7 Algoritmi pe care fiecare programator ar trebui să le cunoască

Ca student la programare, probabil că ați învățat o mulțime de algoritmi diferiți pe parcursul carierei. A deveni competenți în diferiți algoritmi este absolut esențial pentru orice programator.

Cu atât de mulți algoritmi, poate fi o provocare să țineți evidența a ceea ce este esențial. Dacă vă pregătiți pentru un interviu sau pur și simplu vă spălați abilitățile, această listă o va face relativ ușoară. Citiți mai departe pe măsură ce enumerăm cei mai esențiali algoritmi pentru programatori.

1. Algoritmul lui Dijkstra

Edsger Dijkstra a fost unul dintre cei mai influenți informaticieni ai timpului său și la care a contribuit multe domenii diferite ale științei informatice, inclusiv sisteme de operare, construcția compilatorului și multe altele Mai Mult. Una dintre cele mai notabile contribuții ale lui Dijkstra este ingeniozitatea algoritmului său de cale mai scurt pentru grafice, cunoscut și sub numele de Algoritmul de cale mai scurt al lui Dijkstra.

Algoritmul lui Dijkstra găsește cea mai scurtă cale într-un grafic de la o sursă la toate vârfurile graficului. La fiecare iterație a algoritmului, se adaugă un vârf cu distanța minimă de sursă și una care nu există în cea mai scurtă cale curentă. Aceasta este proprietatea lacomă utilizată de algoritmul lui Djikstra.

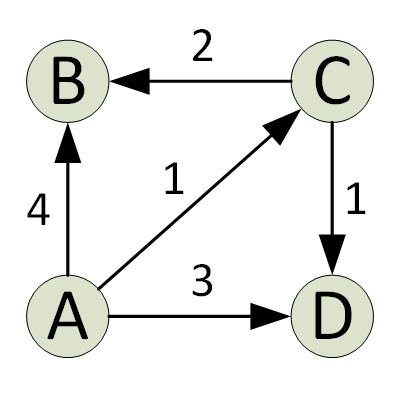
Algoritmul este de obicei implementat folosind un set. Algoritmul lui Dijkstra este foarte eficient atunci când este implementat cu un Min Heap; puteți găsi cea mai scurtă cale în doar O (V + ElogV) timp (V este numărul de vârfuri și E este numărul de muchii dintr-un grafic dat).

Algoritmul lui Dijkstra are limitările sale; funcționează doar pe grafice direcționate și nedirecționate cu margini de greutate pozitivă. Pentru greutăți negative, algoritmul Bellman-Ford este de obicei preferabil.

Întrebările de interviu includ în mod obișnuit algoritmul Djikstra, așa că vă recomandăm să înțelegeți detaliile și aplicațiile sale complexe.

2. Merge Sort

Avem câțiva algoritmi de sortare pe această listă, iar sortarea prin îmbinare este unul dintre cei mai importanți algoritmi. Este un algoritm de sortare eficient bazat pe tehnica de programare Divide and Conquer. În cel mai rău caz, sortarea fuzionării poate sorta numere „n” în doar O (nlogn) timp. Comparativ cu tehnicile de sortare primitive precum Sortare cu bule (care durează O (n ^ 2) timp), sortarea îmbinării este extrem de eficientă.

Legate de: Introducere în algoritmul Merge Sort

În sortare fuzionată, matricea care trebuie sortată este repartizată în mod repetat în subarrays până când fiecare subarray constă dintr-un singur număr. Algoritmul recursiv fuzionează apoi în mod repetat subarrays-urile și sortează matricea.

3. Sortare rapida

Quicksort este un alt algoritm de sortare bazat pe tehnica de programare Divide and Conquer. În acest algoritm, un element este ales mai întâi ca pivot, iar întreaga matrice este apoi partiționată în jurul acestui pivot.

După cum probabil ați ghicit, un pivot bun este crucial pentru un tip eficient. Pivotul poate fi fie un element aleatoriu, elementul media, primul element sau chiar ultimul element.

Implementările quicksort diferă adesea în modul în care aleg un pivot. În cazul mediu, quicksort va sorta o matrice mare cu un pivot bun în doar O (nlogn) timp.

Pseudocodul general al quicksort partiționează în mod repetat tabloul pe pivot și îl poziționează în poziția corectă a subarrayului. De asemenea, plasează elementele mai mici decât pivotul la stânga și elementele mai mari decât pivotul la dreapta.

4. Căutare în adâncime

Căutarea în profunzime (DFS) este unul dintre primii algoritmi grafici învățați studenților. DFS este un algoritm eficient folosit pentru a parcurge sau căuta un grafic. De asemenea, poate fi modificat pentru a fi utilizat în traversarea copacilor.

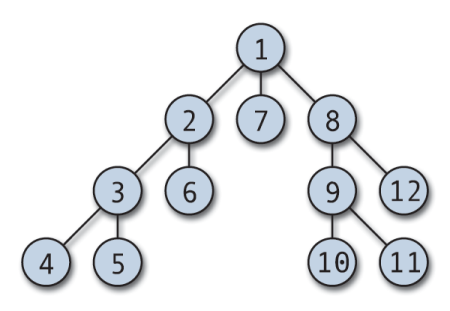
Traversarea DFS poate începe de la orice nod arbitrar și se aruncă în fiecare vârf adiacent. Algoritmul retrocedează atunci când nu există un vârf nevizitat sau când există un punct mort. DFS este de obicei implementat cu o stivă și o matrice booleană pentru a urmări nodurile vizitate. DFS este simplu de implementat și extrem de eficient; funcționează (V + E), unde V este numărul de vârfuri și E este numărul de muchii.

Aplicațiile tipice ale traversării DFS includ sortare topologică, detectarea ciclurilor într-un grafic, căutare de căi și găsirea componentelor puternic conectate.

5. Căutare lățime-întâi

Breadth-First Search (BFS) este, de asemenea, cunoscut sub numele de traversare a ordinii de nivel pentru copaci. BFS funcționează în O (V + E) similar cu un algoritm DFS. Cu toate acestea, BFS folosește o coadă în locul stivei. DFS se scufundă în grafic, în timp ce BFS traversează graficul în sens larg.

Algoritmul BFS utilizează o coadă pentru a urmări vârfurile. Vârfurile adiacente nevizitate sunt vizitate, marcate și în coadă. Dacă vârful nu are vârf adiacent, atunci un vârf este eliminat din coadă și explorat.

BFS este utilizat în mod obișnuit în rețelele peer-to-peer, cea mai scurtă cale a unui grafic neponderat și pentru a găsi arborele minim de întindere.

6. Căutare binară

Căutare binară este un algoritm simplu pentru a găsi elementul necesar într-o matrice sortată. Funcționează împărțind în mod repetat matricea în jumătate. Dacă elementul necesar este mai mic decât cel mai mijlociu element, atunci partea stângă a elementului din mijloc este procesată în continuare; în caz contrar, partea dreaptă este înjumătățită și căutată din nou. Procesul se repetă până când se găsește elementul necesar.

Cea mai proastă situație de timp a căutării binare este O (logn), ceea ce îl face foarte eficient la căutarea matricelor liniare.

7. Algoritmi minimi de copac

Un copac de întindere minim (MST) al unui grafic are costul minim dintre toți copacii de întindere posibili. Costul unui copac întins depinde de greutatea marginilor sale. Este important să rețineți că poate exista mai mult de un copac minim. Există doi algoritmi principali MST, și anume Kruskal și Prim.

Algoritmul lui Kruskal creează MST adăugând marginea cu un cost minim la un set în creștere. Algoritmul sortează mai întâi muchiile după greutatea lor și apoi adaugă muchii la MST începând de la minim.

Este important să rețineți că algoritmul nu adaugă margini care formează un ciclu. Algoritmul lui Kruskal este preferat pentru graficele rare.

Algoritmul lui Prim folosește, de asemenea, o proprietate lacomă și este ideal pentru grafice dense. Ideea centrală în MST-ul lui Prim este de a avea două seturi distincte de vârfuri; un set conține MST în creștere, în timp ce celălalt conține vârfuri neutilizate. La fiecare iterație, este selectată marginea de greutate minimă care va conecta cele două seturi.

Algoritmii minimi de copac sunt esențiali pentru analiza clusterelor, taxonomie și rețele de difuzare.

Un programator eficient este priceput cu algoritmi

Programatorii își învață și își dezvoltă în mod constant abilitățile și există câteva elemente esențiale în care toată lumea trebuie să fie competenți. Un programator calificat cunoaște diferiții algoritmi, beneficiile și dezavantajele fiecăruia și care algoritm ar fi cel mai potrivit pentru un scenariu dat.

O Introducere în Algoritmul Sortare Shell

Deși sortarea shell-ului nu este cea mai eficientă metodă, începătorii au multe de câștigat din practicarea acestuia.

Citiți în continuare

Despre autor